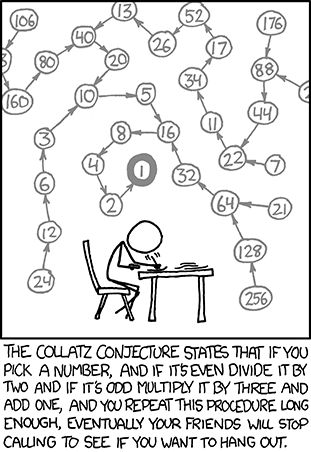
The Collatz Conjecture is a simple mathematical problem that still has no formal proof. So it’s an open problem.
This is how it works:
Choose any positive integer x.
While x > 0, do:
if x is even, divide it by 2 (x = x/2)
if x is odd, multiply it by 3 and add 1 (x = 3x + 1)
The Collatz Conjecture states that no matter what value of x you start with, the sequence will always reach x = 1.
Example:
If x = 10, you get the following sequence:
[10, 5, 16, 8, 4, 2, 1].
If x = 77, you get the following collatz sequence:
[77, 232, 116, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1].
In other words, it doesn’t matter the initial value you pick for x,
you always end up going back to x = 1.
A ruby implementation would look like this:
def collatz n
seq = [n]
until n == 1
n = (n.even?) ? (n / 2) : (3 * n + 1)
seq << n
end
seq
end
A Haskell implementation[1] could look like this:
chain :: (Integral a) => a -> [a]
chain 0 = error "Invalid!"
chain 1 = [1]
chain x
| even x = x:chain (x `div` 2)
| odd x = x:chain (x*3 + 1)
[1] Source: a gist that is not available anymore.
Did you like this article? Then you're gonna love these other ones: